SKT_ICT_코딩테스트 #4. 대체 문제 백준_20188_등산마니아

( 문제 )

등산 마니아 서브 태스크

시간 제한메모리 제한제출정답맞힌 사람정답 비율

2 초

512 MB

745

287

228

42.617%

문제

동네 뒷 산에는 등산로가 있다. 등산로는 N개의 작은 오두막들이 N −1개의 오솔길로 이어진 형태이다. 한 오솔길은 두 개의 오두막을 양 방향으로 연결한다. 한 오솔길의 길이는 1이다. 어떤 오두막에서도 다른 모든 오두막으로 하나 이상의 오솔길을 따라 이동하는 것이 가능하다. 오두막들은 1번부터 N번까지 번호가 붙어 있으며, 1번 오두막이 산 정상에 있다. 1번 오두막에서 다른 오두막으로 가는 가장 짧은 길을 따라가면서 거치는 모든 오솔길들은 항상 산을 내려가는 방향이다.

철수는 등산 마니아이다. 철수가 한 오두막에서 다른 오두막으로 갈 때는 항상 산 정상을 거치는 가장 짧은 길을 따라간다. 이렇게 간 길의 다양성은 길에 포함된 오솔길의 개수로 정의된다. 두 번 이상 지나간 오솔길은 한 번만 센다는 것에 주의하라.

아래 그림은 가능한 하나의 상황을 보여 준다. 산 정상에 1번 오두막이 있고 3번 오두막과 4번 오두막이 오솔길로 이어져 있다.

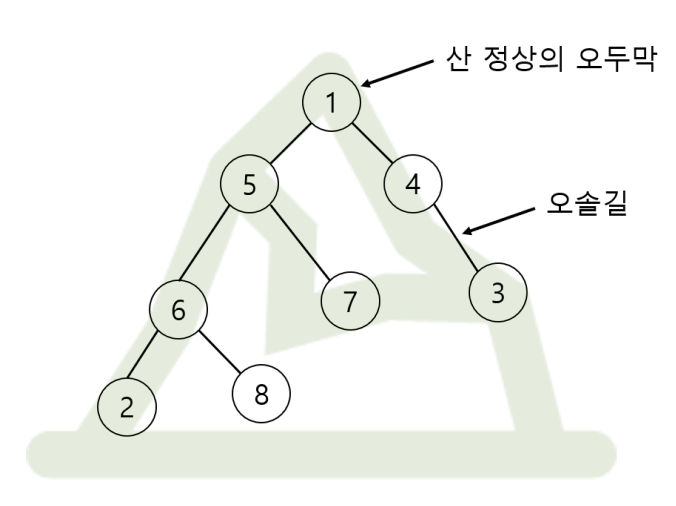
아래 그림은 2번 오두막에서 7번 오두막으로 가는 가장 짧은 길을 보여준다.

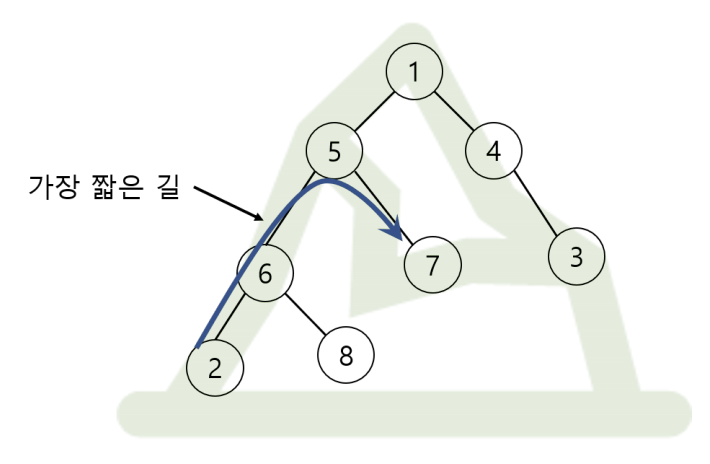
아래 그림은 2번 오두막에서 7번 오두막으로, 정상을 거쳐서 가는 가장 짧은 길을 보여 준다.

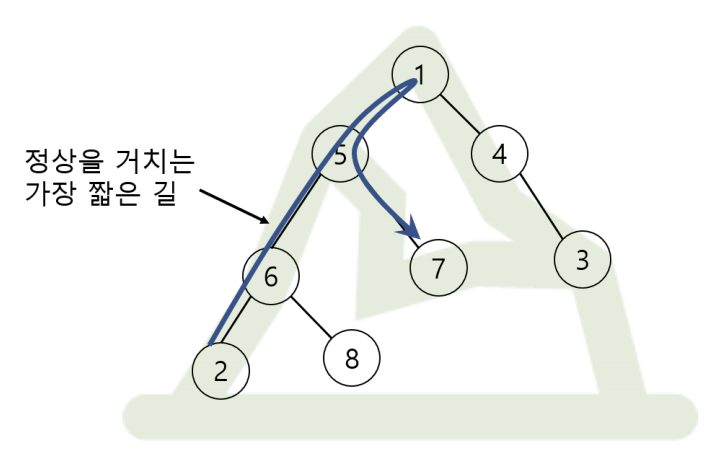
등산로의 구성을 입력으로 받아 모든 가능한 i, j의 쌍에 대해서(1 ≤ i < j ≤ N), 철수가 i번 오두막에서 j번 오두막으로 가는 길의 다양성의 총합을 계산하는 프로그램을 작성하라.

입력

첫 번째 줄에 N이 주어진다. 다음 N −1개의 줄에 오두막 번호 두 개가 공백 하나를 사이에 두고 주어진다. 두 오두막이 오솔길로 이어져 있다는 뜻이다.

출력

첫 번째 줄에 문제의 정답을 출력한다.

제한

• 2 ≤ N ≤ 300 000

서브 태스크

번호배점제한

1	8	1번 오두막과 2번 오두막, 2번 오두막과 3번 오두막, · · ·, 과 같이 모든 i (1 ≤ i ≤ N − 1)에 대해 i번 오두막이 i + 1번 오두막과 오솔길로 이어짐.
2	11	1번 오두막과 다른 모든 오두막이 각각 오솔길로 이어짐.
3	19	1번 오두막에서 산을 내려가는 방향으로 갈 때, (1번 포함) 모든 오두막에서 내려가는 방향의 오솔길은 2개이거나 0개이다. 또, 내려가는 방향의 오솔길이 0개인 모든 오두막은 1번 오두막에서의 거리가 동일하다.
4	17	N ≤ 100
5	14	N ≤ 5 000
6	31	추가 제약 조건 없음

예제 입력 1 복사

3
1 2
2 3

예제 출력 1 복사

5

예제 입력 2 복사

8
6 2
7 5
3 4
5 6
1 5
4 1
8 6

예제 출력 2 복사

84

---

( 문제 해설 )

 

그림으로 문제 풀이하겠습니다.

그림_1

그림_2

그림_3

그림_4

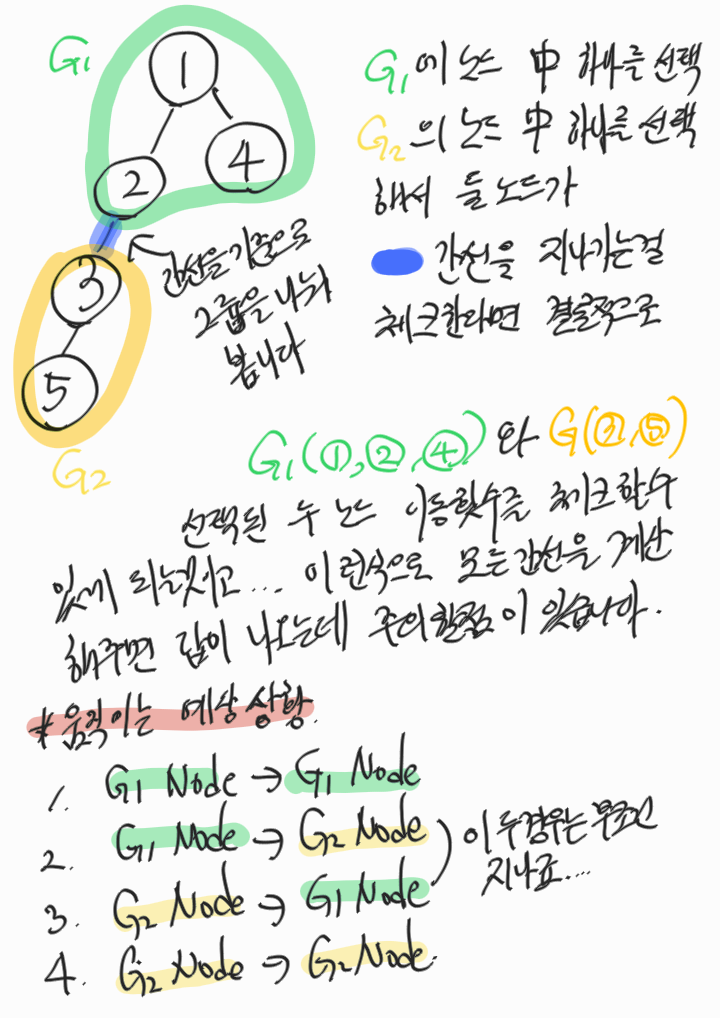
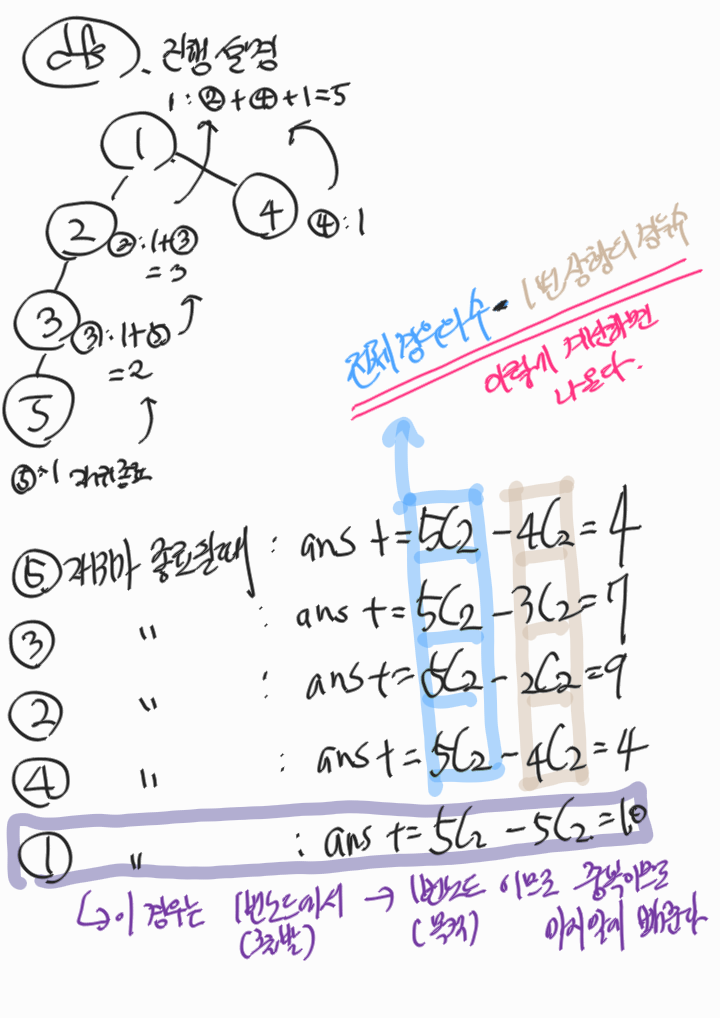
(정리)

 

이런 식을 문제풀이를 합니다.

정리하면 출발지에서 목적지로 가는데 중간에 루트 노트 1을 찍고 목적지로 가야 한다. 이런 경우를 카운트 한 번!

근데 결국에는 두 개의 노드를 선택하는 이동하는 경우가 아닌가?

문제에는 루트 노드 1을 찍어야 하니까 노드를 선택해서 그 부분을 염두에 두면서 간선을 기준으로 그룹을 나눠 간선의 이용 수를 계산해서 문제 풀이를 그나마 쉽게 하는 겁니다.

 

혹시 문제가 전혀 파악되지 않아서 돌아다니다 이 글을 보셨음에도 문제가 잘 이해가 안 간다면 죄송합니다.

저의 능력 부족인데.. 어쨌든 제가 최대한 이해한 걸 바탕으로 풀이해보았습니다,

아래는 해당 문제 코드입니다.

 

---

[ 코드 ]

 

import sys
sys.setrecursionlimit(10 ** 6)


def init():
    N = int(input())
    tree = [[] for i in range(30001)]
    for e in range(N - 1):
        u, v = map(int, input().split())
        tree[u].append(v)
        tree[v].append(u)
    group = [0] * 30001
    ans = 0
    return N, tree, group, ans


def cnt(n):
    return n * (n - 1) // 2


def dfs(cur, prev):
    global ans

    group[cur] = 1  # 서브트리에 자기 자신 추가
    for nxt in tree[cur]:
        if nxt != prev:
            group[cur] += dfs(nxt, cur)

    # print(group, cur)
    ans += cnt(N) - cnt(N - group[cur])
    # print(cur, group[cur], ans, cnt(N) - cnt(N - group[cur]))
    return group[cur]


N, tree, group, ans = init()


"""
간선별로 그륩을 나누고 그 간선이 얼마나 사용됐는지 구하고 그 값을 모두 더하는 문제

(예시에 이용한 입력)
5
1 2
2 3
1 4
3 5

"""

dfs(1, 0)
print(ans - cnt(N))

 

---

후기

 

아이고 대가리 깨질 거 같은 문제

근데 문제를 이해하고 풀 수 있었습니다

물론 다른 분들의 자료를 참고했지만요

그래도 성취감이 있습니다

좋네요

skt 4번 솔한걸로 치겠습니다 크크루크크 ㄹㅇㅋㅋ