백준 2141번 - 우체국 문제 풀이
2025. 9. 4. 21:04ㆍTest
728x90
📌 가중치 중앙값(Weighted Median)과 우체국 문제 풀이 과정
1. 문제 배경
우체국 문제(백준 2141번)는 다음과 같은 식으로 정의됩니다.
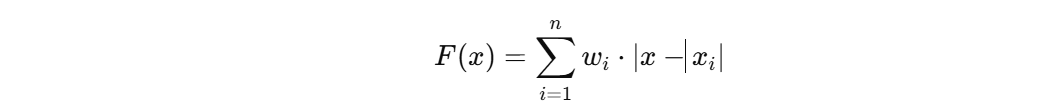
- : 마을의 좌표
- : 마을의 인구 수
- F(x): 특정 위치 에 우체국을 세웠을 때, 모든 마을까지의 인구 가중 거리의 합
우리가 구해야 하는 것은 F(x)가 최소가 되는 최적의 우체국 위치입니다.
2. 수학적 원리 — 왜 가중치 중앙값인가?
(1) 절댓값 미분
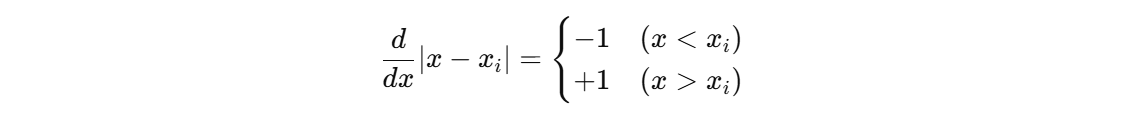
(2) 가중치 포함
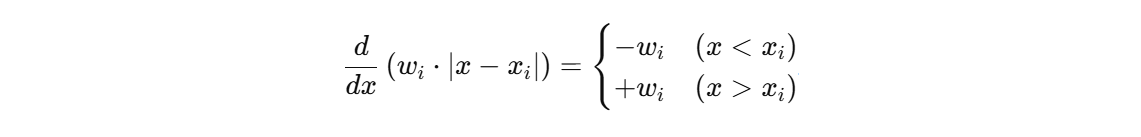
(3) 전체 미분

(4) 정리
전체 인구를 ,
기준 왼쪽 인구를 라 하면
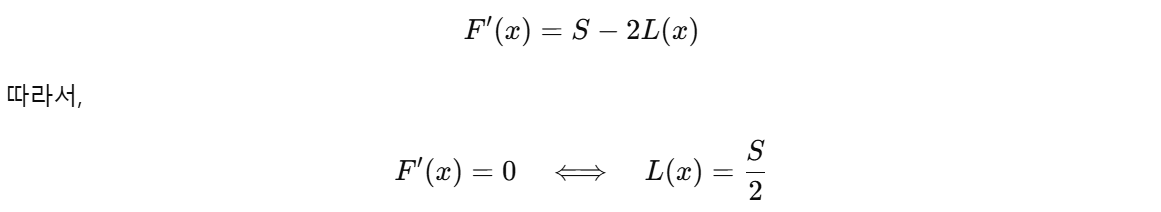
4) 정리
전체 인구 합을 , x 기준 왼쪽 인구 합을 라 하면
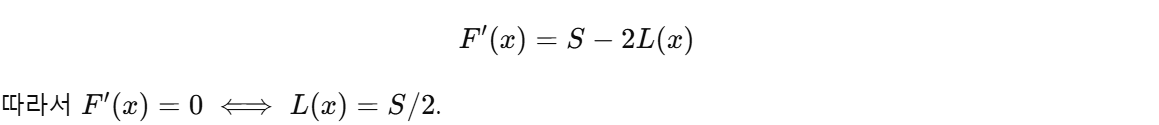
즉, 전체 인구의 절반 이상이 모이는 위치가 최적의 우체국 위치입니다.
이를 **가중치 중앙값(Weighted Median)**이라 합니다.
3. 알고리즘 구현
핵심 아이디어
- 마을을 좌표 기준으로 정렬한다.
- 인구를 누적합하면서, 누적 인구가 전체 인구의 절반 이상이 되는 순간 그 위치가 답이다.
코드
def solve_weighted_median(positions, weights):
"""
F'(x) = S - 2L(x) 원리에 따른 우체국 위치 찾기
"""
# (위치, 인구) 묶어서 좌표 기준 정렬
houses = sorted(zip(positions, weights), key=lambda x: x[0])
total_population = sum(weights)
target = (total_population + 1) // 2 # 절반 이상
cumulative_population = 0
for pos, weight in houses:
cumulative_population += weight
if cumulative_population >= target:
return pos4. 코드 작성 시 주의할 점 ⚠️
- 정렬 기준 명시하기
단순 sort()는 같은 좌표가 있을 때 가중치까지 비교해서 순서가 바뀔 수 있습니다.
→ 반드시 key=lambda x: x[0]로 좌표 기준 정렬을 명확히 해야 합니다. - 절반 계산 방식
total / 2로 실수를 쓰면 애매한 경우가 생길 수 있습니다.
→ (total + 1) // 2로 정수 올림을 해 주는 것이 안전합니다. - 출력 처리
함수만 정의하면 결과가 안 보입니다.
→ 반드시 print(result) 해 주어야 합니다.
5. 예시 실행
입력
3
1 2
2 4
10 3- 전체 인구: 9
- 절반 이상: 5명
누적합
- 좌표 1: 인구 2 (누적 2) < 5
- 좌표 2: 인구 4 (누적 6) ≥ 5 → 정답 = 2
출력
26. 결론
- 우체국 문제는 결국 가중치 중앙값을 찾는 문제입니다.
- 수학적으로는 에서 도출됩니다.
- 구현에서는 좌표 기준 정렬 + 누적합만 하면 해결됩니다.
728x90
'Test' 카테고리의 다른 글
| 백준 - 리그 오브 레전설 (Small) 풀이 정리 (3) | 2025.08.24 |
|---|---|
| 기업 코테 풀이 (1) | 2023.01.20 |
| kstec 코테 후기 (1) | 2022.10.29 |
| 엘리스 코딩 테스트 후기 + 못푼거 문제 풀이 (0) | 2022.08.20 |
| sql문제를 코테에서 처음 풀이 성공함 (0) | 2022.07.03 |