( 문제 설명 )
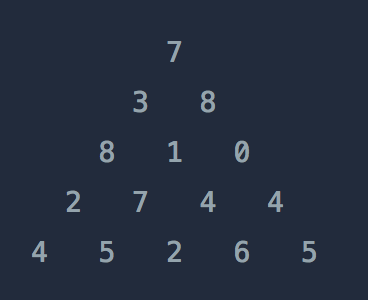
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
( 문제 해설 )
dp를 주제로 나와있는 문제니까 dp로 푸는 게 좋다
예제를 예시로 설명을 하겠다.
( 생각 알고리즘 )
0. 산을 타듯이 위로 올라가는게 좋아 보인다. => 입력된 삼각형 배열을 반대로 정렬
1. 예시에서 산의 크기는 5이다. 그리고 현재 배열 i와 다음 배열 i + 1을 비교할 거니까 삼각형 - 1 만큼 for문을 돌 것이다.
len(triangle) - 12. 마찬가지로 좌우의 값을 비교하여 큰값을 더해서 올릴 거기 때문에 삼각형 - 1만큼 순회한다 그리고!! 위로 갈수록 하나씩 작아지므로 현재 배열이 순회 되는 만큼 줄여야 한다는 뜻이다 => 삼각형 - 1 - 현재순회(i) 이 된다
len(triangle) - i - 13. 이렇게 for문을 돌 것이고 양쪽에서 큰 값을 올릴 거므로 max(dp[i][j], dp[i][j+1]) 이 되고 위로 올릴값은 dp[i+1][j]가 될 것이다.
4. 결론적으로, dp[i + 1][j] = max(dp[i][j], dp[i][j+1]) 이 될 것이다.
[ 코드 ]
# 2. 정수 삼각형
def solution(triangle):
triangle.sort(key=lambda x: len(x), reverse=True)
dp = []
for i in range(len(triangle)):
dp.append(triangle[i])
for i in range(len(triangle) - 1):
for j in range(len(triangle) - i - 1):
dp[i + 1][j] += max(dp[i][j], dp[i][j + 1])
answer = max(dp)
return answer[0]
triangle = [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
sol = solution(triangle)
print(sol)후기
개인적으로 이런 dp문제가 그나마 좋다.
간단하게 그림을 그려보고 로직을 만드면 그나마 쉽게 풀린다.
너무 많은 수학적인 계산이 필요하지도 않고요.
'프로그래머스 고득점kit > 동적계획법' 카테고리의 다른 글
| [고득점 kit]_동적계획법_#4. 도둑질 (0) | 2022.04.24 |
|---|---|
| [고득점 kit]_동적계획법_#3. 등굣길 (0) | 2022.04.22 |
| [고득점 kit]_동적계획법_#1. N으로 표현 (0) | 2022.04.20 |

