2022. 4. 22. 21:38ㆍ프로그래머스 고득점kit/동적계획법
(문제 설명)
계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.
아래 그림은 m = 4, n = 3 인 경우입니다.
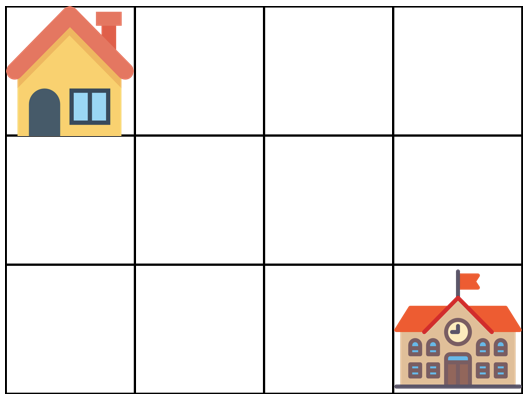
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.
격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.
제한사항- 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
- m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
- 물에 잠긴 지역은 0개 이상 10개 이하입니다.
- 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.
| 4 | 3 | [[2, 2]] | 4 |

예제 1로. 설명을 하겠다.
( 생각 알고리즘 )
1. 이동은 오른쪽 아래만 가능하다.
2. 시작위치에서 목표지점까지 가능한 경우의 수를 구하는 문제
### 이 문제는 고등학교 경우의 수 문제에서 자주 나왔던 방법을 dp화 시키면 됩니다.
이런 식으로 문제 푸신 걸 떠올려 보세요!

이렇게 문제 푸는 방식을 저희는
1. 이동은 오른쪽 아래만 가능하다. 을 고려하여 문제를 푸시면 됩니다
아래는 예시1의 진행 과정입니다.
진행 과정을 보여드리겠습니다.
| # 처음 [0, 0, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 0, 0] [0, 1, 0, 0, 0] [0, 1, 1, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 0] [0, 1, 0, 0, 0] [0, 1, 1, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 0] [0, 1, 0, 1, 0] [0, 1, 1, 0, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 0] [0, 1, 0, 1, 0] [0, 1, 1, 2, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 1] [0, 1, 0, 1, 0] [0, 1, 1, 2, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 1] [0, 1, 0, 1, 2] [0, 1, 1, 2, 0] [0, 0, 0, 0, 0] [0, 1, 1, 1, 1] [0, 1, 0, 1, 2] [0, 1, 1, 2, 4] |
이런 식으로 진행하는 거고 초기 테두리 0 값은 머냐고 하면 저렇게 0을 둘러치지 않으면 인덱스 에러가 나기 때문이죠 때문에 아무런 경우의 수에 추가되지 않는 값인 0을 겉에 둘러쳐서 계산을 쉽게 하기 위함입니다.
[ 코드 ]
# 3_1. 등굣길
def solution(m, n, puddles):
# 코드 간단 설명
# +1을 해주는 이유는 dp계산에 있어서 index error를 없에기 위함
# 상, 좌에 물로 덮어진 맵을 만든다고 생각하면 된다.
# 물을 0으로 하면 더해도 경우의 수를 계산하지 않는 상황이 되기 때문
dp = [[0] * (m + 1) for i in range(n + 1)]
# 시작
dp[1][1] = 1
for j in range(1, m + 1):
for i in range(1, n + 1):
# 시작 값을 살리기 위해
if i == 1 and j == 1:
continue
if [j, i] in puddles:
dp[i][j] = 0
else:
# 아래, 오른쪽의 경우의 수의 합이 지금 위치의 경우의 수
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
answer = dp[n][m] % 1000000007
return answer후기
좌표를 순회할 때는 우리가 기존에 생각하는 좌표는
for문을 순회할 때의 인덱스 [i][j]랑은 반대라는 것
이점은 항상 문제 풀면서 생각하자. 항상 헷갈림 ㅋㅋ
인덱스 오류의 주범...
'프로그래머스 고득점kit > 동적계획법' 카테고리의 다른 글
| [고득점 kit]_동적계획법_#4. 도둑질 (0) | 2022.04.24 |
|---|---|
| [고득점 kit]_동적계획법_#2. 정수 삼각형 (0) | 2022.04.21 |
| [고득점 kit]_동적계획법_#1. N으로 표현 (0) | 2022.04.20 |