2022. 5. 17. 19:56ㆍ프로그래머스 고득점kit/그래프
(문제 설명)
원점(0,0)에서 시작해서 아래처럼 숫자가 적힌 방향으로 이동하며 선을 긋습니다.
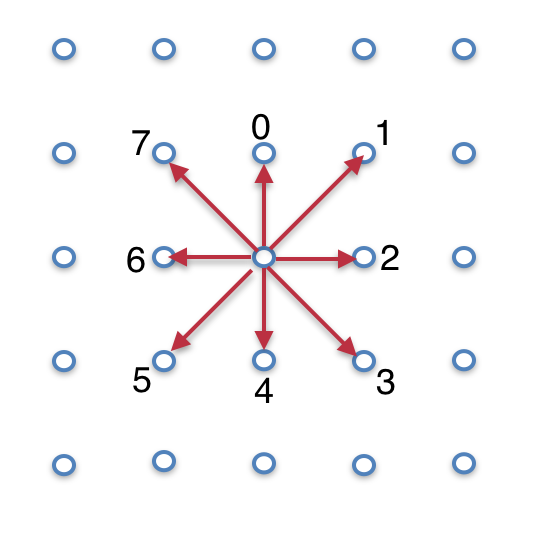
ex) 1일 때는오른쪽 위로 이동
그림을 그릴 때, 사방이 막히면 방 하나로 샙니다.
이동하는 방향이 담긴 배열 arrows가 매개변수로 주어질 때, 방의 개수를 return 하도록 solution 함수를 작성하세요.
- 배열 arrows의 크기는 1 이상 100,000 이하 입니다.
- arrows의 원소는 0 이상 7 이하 입니다.
- 방은 다른 방으로 둘러 싸여질 수 있습니다.
| [6, 6, 6, 4, 4, 4, 2, 2, 2, 0, 0, 0, 1, 6, 5, 5, 3, 6, 0] | 3 |
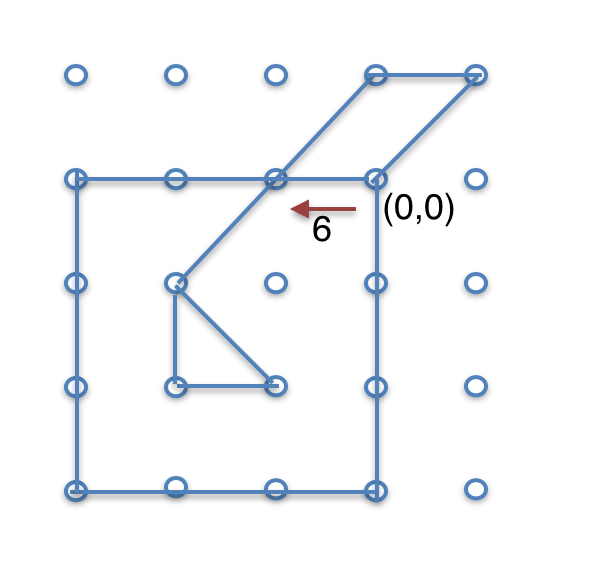
- (0,0) 부터 시작해서 6(왼쪽) 으로 3번 이동합니다. 그 이후 주어진 arrows 를 따라 그립니다.
- 삼각형 (1), 큰 사각형(1), 평행사변형(1) = 3
( 문제 해설 )
0. 8방향으로 움직일 때 8방향의 중 한 방향으로 이동하는 이동지시가 주어질 때 방의 개수 즉, 도형이 만들어지는 개수를 리턴하는 문제.
[6, 6, 6, 4, 4, 4, 2, 2, 2, 0, 0, 0, 1, 6, 5, 5, 3, 6, 0]
1. 이문제가 주어진 예제 값을 공책에다가 한 땀 한 땀 그려보면 내가 지나간 좌표에 다시 한번 도착하면 도형이 만들어진다는 것을 알 수 있습니다.
2. 그런데 문제가 하나 있죠. 그런 상황 중에서 도형이 안 만들어지는 상황이 있습니다.
3. 바로 떠오르는 건 좌우 반복 같은 움직임입니다. 때문에 내가 지나간 자리를 다시 도착하되 그 지점 바로 이전 지점의 좌표이면 안됩니다. 이 부분을 예외처리해주어야 합니다.
4. 그 이후 예외처리가 하나 더 있습니다. 바로 모래시계 모양입니다.
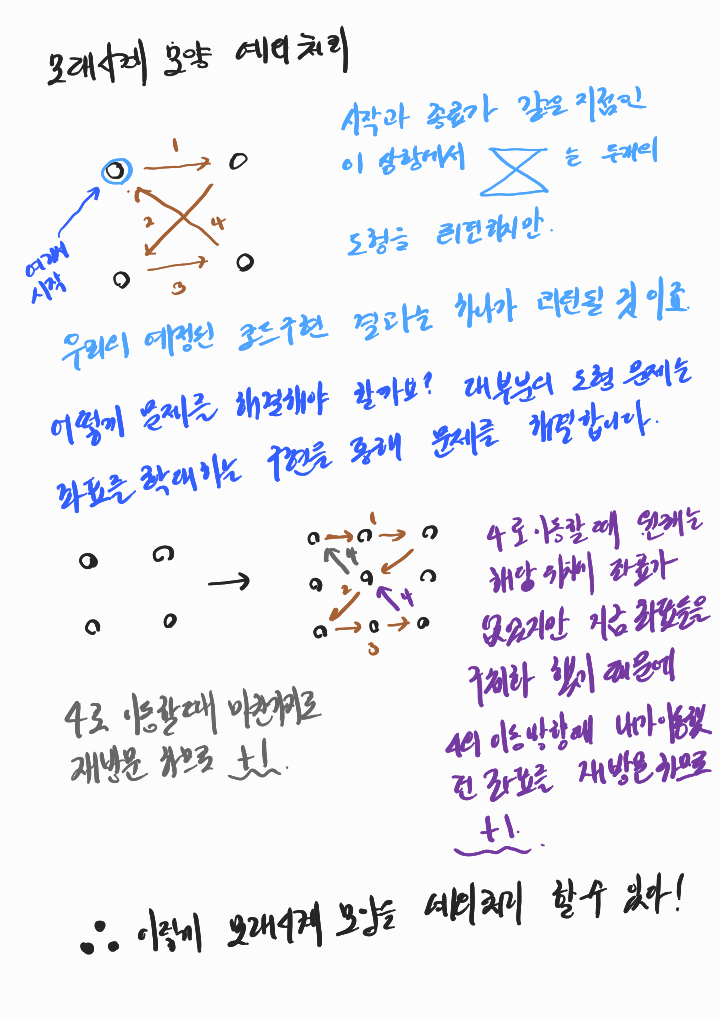
5. 이렇게 한 번의 좌표 움직임을 두 번으로 나눠서 코드를 구현하면 3번에서 짜둔 좌우 반복 예외처리 코드가 쓸모가 없어질 것이다 이 부분은 어떻게 해결해야 할까?
5-1. 단순히 전에 이동한 지점이 아니라면 +1을 해주는 식의 코드는 통하지 않는다!! 하려면 머리가 복잡하다. 2개의 텀을 둬서 기억해야 하니까.... 정말 어떻게 해야 할까?
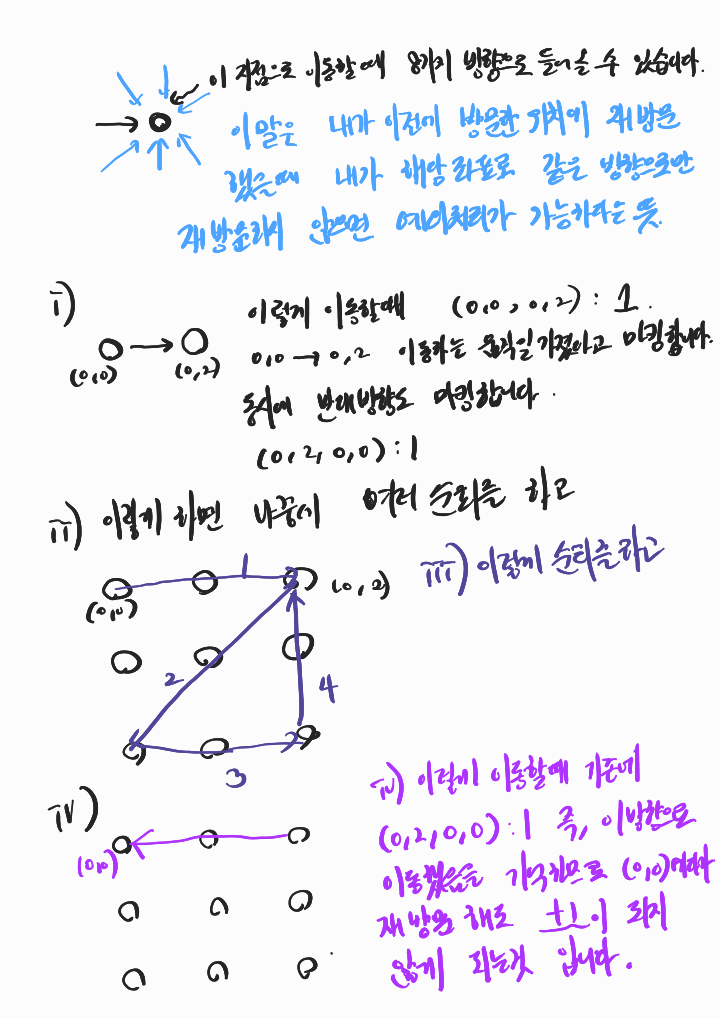
6. 이렇게 두 상황을 고려하려 재방문했을 때 +1을 해주는 코드를 짜 보자!!
[ 코드 ]
# 3. 방의 개수
from collections import defaultdict
dx = [-1, -1, 0, 1, 1, 1, 0, -1]
dy = [0, 1, 1, 1, 0, -1, -1, -1]
def solution(arrows):
answer = 0
courseGraph = defaultdict(int)
cur = [0, 0]
c_x = cur[0]
c_y = cur[1]
# visited[c_x][c_y] = 1
visited = set([(0, 0)])
prev_x = c_x
prev_y = c_y
for i in range(len(arrows)):
idx = arrows[i]
for _ in range(2):
c_x += dx[idx]
c_y += dy[idx]
if (c_x, c_y) in visited:
# 좌우 반복문제를 방향을 기억하는 방식으로 문제를 해결했다.
if courseGraph[(c_x, c_y, prev_x, prev_y)] == 0:
print(courseGraph)
answer += 1
elif (c_x, c_y) not in visited:
visited.add((c_x, c_y))
courseGraph[(c_x, c_y, prev_x, prev_y)] = 1
courseGraph[(prev_x, prev_y, c_x, c_y)] = 1
prev_x = c_x
prev_y = c_y
return answer후기
오늘 드디어!!! 고득점 키트의 해설 풀이를 모두 끝냈습니다.
지금도 계속 기출 코테를 풀고 있는데, 이제 이문제들의 해설로 이어 가겠습니다.
복습 겸으로요!!
'프로그래머스 고득점kit > 그래프' 카테고리의 다른 글
| Union-Find Algorithm (유니온 파인드 알고리즘) 탬플릿 코드 (0) | 2024.07.21 |
|---|---|
| 고득점kit) 그래프 #2. 순위 (0) | 2022.05.12 |
| 고득점kit) 그래프 # 1. 가장 긴 노드 (1) | 2022.05.11 |